人狼::人狼BBS
人狼BBSというものをご存知だろうか.
村人の中に人狼が紛れ込んでいて,その人狼が毎晩一人を喰らう.村人は誰が人狼かを推理しつつ疑わしいものを毎日ひとりずつ吊るし上げていく.最終的に,人狼を全滅させれば村の勝ち,村人が人狼以下になったら人狼の勝ち,というゲームをBBS形式で進める.
人狼かどうかを占える占い師や,死んだ人が人狼かどうかが分かる霊能者といった能力を持った人がいるので,その人を頼りに村人は人狼を探し出すことになる.ただ,誰がどの能力を持っているかは全く分からないため,占い師が出てきてもまずそれが本物かを見極めなくてはならない.
という知的(?)なゲームであるが,それぞれに村長や神父,木こり,村娘,爺といったアバターが与えられ,そのロールプレイをするのも一つの楽しみとなっている.
んで,何が最適な戦略かを計算してみようかと思ったんだけど,なんとも大変そうなのでとりあえず簡単に「不死身の占い師が居る場合」と「占い師不在の場合」の勝率を計算してみた.
一応戦略ルールとして,
1.狼は確定白が居れば,それを襲う(グレーを狭くするのは自分の占われる確率が高くなるので不利)
2.吊り先はグレーからランダムで選ぶ.狼の議論誘導は考慮しない
3.占い先はグレーからランダムで選ぶ.狼の議論誘導は考慮しない
4.吊り先と襲う先は被らないものとする(村で吊り先を一致指定する場合被らないはず,各自投票の場合狼の組織票が生きるので村に不利だと思われる.ってそうも言い切れない部分もあるが)
を想定し,二日目からスタートするものとする(つまり占い判定が一つ出てから吊り→人喰いが行われ,それが1ターン).
1つ目のグラフは不死身の占い師がいる場合.真占い師を信用し,最後まで守ることができれば勝率は限りなく高いということを示す.
2つ目のグラフは占い師不在の場合.真占い師が居なくなると,圧倒的に人狼が有利であることを示す.
って当たり前のことやんか!
ちなみに真占い師+白確定2人とかになるとほぼ確実に村が勝てるみたい.つまり占い師+共有者二人COがあった場合,人狼は必ず対抗COを出さなくてはなりません.人狼側としては占い師をいかに表に出してきて殺すかが常に重要なので,とりあえず死んでも構わない(霊能者に疑われない)狂人の占い師COは必須のような気がするけどどうでしょ.
不思議なのは村人の人数に対して村の勝利確率が単調増加でない点です.
多分「村人2:人狼1」よりも「村人3:人狼1」の方が勝率が低いということに起因していると思うんだけど,摩訶不思議な感じ.これだと故意に突然死を起こしたほうが有利になる事があるってことだ.てかどっか間違ってるかな?
ちなみに人狼の勝利条件を「村人<=人狼」ではなく「村人<人狼」にすれば(つまり村人が全滅するまでという条件にすれば),村人の数に対して単調増加になるようだ.
とりあえずこのコードが怪しい部分もあるので,ご指摘頂けたら幸いです.
ついでに戦略についていろいろ(具体的な数字を出して)研究しているサイトがあったら教えてー.
何故かプレイ開始してみたんで(暇人だなオイ).
あと,全然麻雀的な内容じゃないですが,こういうゲームの戦略的な話題は面倒なので全て麻雀カテゴリに含めることにしました.合掌.
村人の中に人狼が紛れ込んでいて,その人狼が毎晩一人を喰らう.村人は誰が人狼かを推理しつつ疑わしいものを毎日ひとりずつ吊るし上げていく.最終的に,人狼を全滅させれば村の勝ち,村人が人狼以下になったら人狼の勝ち,というゲームをBBS形式で進める.
人狼かどうかを占える占い師や,死んだ人が人狼かどうかが分かる霊能者といった能力を持った人がいるので,その人を頼りに村人は人狼を探し出すことになる.ただ,誰がどの能力を持っているかは全く分からないため,占い師が出てきてもまずそれが本物かを見極めなくてはならない.
という知的(?)なゲームであるが,それぞれに村長や神父,木こり,村娘,爺といったアバターが与えられ,そのロールプレイをするのも一つの楽しみとなっている.
んで,何が最適な戦略かを計算してみようかと思ったんだけど,なんとも大変そうなのでとりあえず簡単に「不死身の占い師が居る場合」と「占い師不在の場合」の勝率を計算してみた.
一応戦略ルールとして,
1.狼は確定白が居れば,それを襲う(グレーを狭くするのは自分の占われる確率が高くなるので不利)
2.吊り先はグレーからランダムで選ぶ.狼の議論誘導は考慮しない
3.占い先はグレーからランダムで選ぶ.狼の議論誘導は考慮しない
4.吊り先と襲う先は被らないものとする(村で吊り先を一致指定する場合被らないはず,各自投票の場合狼の組織票が生きるので村に不利だと思われる.ってそうも言い切れない部分もあるが)
を想定し,二日目からスタートするものとする(つまり占い判定が一つ出てから吊り→人喰いが行われ,それが1ターン).
augur[V_] := Module[{m, m2, a, n, n2},
{m, m2, a, n, n2} = V;
If[m2 < 0, m += m2; m2 = 0];
If[n2 < 0, n += n2; n2 = 0];
Which[
m < 0, 0,
a + m + m2 <= n + n2, 0,
n + n2 == 0, 1,
a == 0 || m == 0 || n == 0, hang[V],
True, If[m > 1, {m - 1, 1, n}, {m, 0, n}]/(m+n).
{hang[{m-1,m2+1,a,n,n2}],hang[V],hang[{m,m2,a,n-1,n2+1}]}
]
];
hang[V_] := Module[{m, m2, a, n, n2},
{m, m2, a, n, n2} = V;
Which[
m < 0, 0,
m + n == 0, If[m2 + a > n2, 1, 0],
True,
If[n2 > 0, {0, 1}, {m, n}/(m + n)].
{augur[{m - 1, m2 - 1, a, n, n2}],
augur[{m, m2 - 1, a, n, n2 - 1}]}
]
];
(* 村人(灰)m, 村人m2(白), 人狼(灰)n 村の勝率を返す*)
vilwolf[m_, m2_, n_] := augur[{m, m2, 0, n, 0}];
(* 村人(灰)m, 村人m2(白), 占い師1,
人狼(灰)n 村の勝率を返す(占い師は不死身とする) *)
vilwolf2[m_, m2_, n_] := augur[{m - 1, m2, 1, n, 0}];
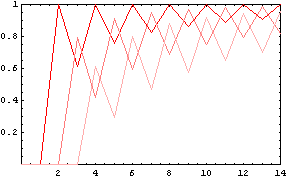
(* 占い師有りの勝率(横軸:村人の数),色が濃い方から狼1,2,3匹の場合 *)
Show[Table[
ListPlot[Table[{x, vilwolf2[x, 0, w]}, {x, 0, 14}],
PlotJoined -> True, PlotStyle -> {RGBColor[1, 1-1/w, 1-1/w]}],
{w, 1, 3}],
PlotRange -> {{0, 14}, {0, 1}}, Frame -> True];
(* 占い師なしの勝率(横軸:村人の数),色が濃い方から狼1,2,3匹の場合 *)
Show[Table[
ListPlot[Table[{x, vilwolf[x, 0, w]}, {x, 0, 14}],
PlotJoined -> True, PlotStyle -> {RGBColor[1, 1-1/w, 1-1/w]}],
{w, 1, 3}],
PlotRange -> {{0, 14}, {0, 1}}, Frame -> True];
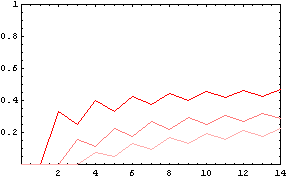
横軸が村人の数(占い師は含む,人狼は含まない),縦軸が村が勝つ確率.
1つ目のグラフは不死身の占い師がいる場合.真占い師を信用し,最後まで守ることができれば勝率は限りなく高いということを示す.
2つ目のグラフは占い師不在の場合.真占い師が居なくなると,圧倒的に人狼が有利であることを示す.
って当たり前のことやんか!
ちなみに真占い師+白確定2人とかになるとほぼ確実に村が勝てるみたい.つまり占い師+共有者二人COがあった場合,人狼は必ず対抗COを出さなくてはなりません.人狼側としては占い師をいかに表に出してきて殺すかが常に重要なので,とりあえず死んでも構わない(霊能者に疑われない)狂人の占い師COは必須のような気がするけどどうでしょ.
不思議なのは村人の人数に対して村の勝利確率が単調増加でない点です.
多分「村人2:人狼1」よりも「村人3:人狼1」の方が勝率が低いということに起因していると思うんだけど,摩訶不思議な感じ.これだと故意に突然死を起こしたほうが有利になる事があるってことだ.てかどっか間違ってるかな?
ちなみに人狼の勝利条件を「村人<=人狼」ではなく「村人<人狼」にすれば(つまり村人が全滅するまでという条件にすれば),村人の数に対して単調増加になるようだ.
とりあえずこのコードが怪しい部分もあるので,ご指摘頂けたら幸いです.
ついでに戦略についていろいろ(具体的な数字を出して)研究しているサイトがあったら教えてー.
何故かプレイ開始してみたんで(暇人だなオイ).
