なんか知らない人のblogに，僕の自動打ちソフトの事が書いてあった．

ところで、上記の自動打ちプログラムは、ちょっとひどい。
まあ、自分でプログラムを作ったら、当初もっとひどいかもしれないが。
それでも、けっこう、先読みしたりしてるみたいだ。
基本的に、評価関数の設計が間違っていると思うのだが。
へんな孤立牌に固執して、両面ターツを落としていったり、へたすると、出来面子
を落としていったりする。牌の残り枚数が一定を切った次点で、オリモードになる
のかな、とも思うが、いわゆる牌効率がわるすぎて、ほとんど聴牌しないのに、
さらにオリてどうするのだろう。聴牌していて、役なしなのに、なかなかリーチ
をかけないのも解せない。そして、しばらくするとオリモードになるのか、手牌
はバラバラに。
そのくせ、見えてる牌から、牌の残り確率なんかを計算しているが。牌の残り
確率を後回しにしてでも、もっと牌効率をよくしないと、まず、テンパらない。
テンパらない麻雀は１００％負ける。

ガガーン．確かによええけどよお．
てことで，verupしました．
ここからどうぞ．
作者からのコメント:
ムシャクシャしてついカッとなってやった．悪気はない．今は反省している．

相変わらず鳴けませんが，前回よりは強くなったはずです．というより前のは弱すぎた．

前がダメだったのは，ムダヅモを考慮しまくってたところ．それが一番大きいかなあ．
他にも細かい改良しまくったので，具体的にどこを直したとか覚えてません．

というよりほぼ一年ぶりにソースを弄ろうとしたら，model2-1(これが確か前回のもの)の他にmodel3とかmodel4があった．なんだろうこれは？と思い見てみたら他のアルゴリズムを試した書きかけだった．試しに打たせてみたら全部ツモ切り．やる気ねええええ．
解読してmodel4ベースにしようかと思ったけど，やっぱり大変そうなので諦めてmodel2ベースでやることにした．model2は切らずにどんどんツモっていって和了まで行ってから不要牌にその手の価値を分配させてやるアルゴリズム．ただ，最後に何をつもるかが確定しないので，普通にやると平和等の和了の形が正しく判定できない．model3は確か和了までじゃなく，聴牌までツモりまくる手法．こうすると待ちの形まで正確に評価できる．model4はツモ→打牌を純粋に繰り返すアルゴリズム．あっという間に組合せが発散するのでお勧めできない．
model3,4ともに超作りかけだったし，計算量的にmodel2が一番スマートなのでmodel2を改良していくことに落ち着いた．

計算量は重要である．
上のblogで「評価関数の設計が間違っているのではないか」と書いてあるが，その通りで評価関数を作るのが難しい(というよりそこしか問題はない)．最も単純かつベストな評価関数は和了形の点数とそこまでに到達する可能性を使ったものだろう．これを使うと結局和了きるまでシミュレートしなくてはならないため，膨大な計算が必要になる．それこそmodel4の方法で(明らかな無駄ヅモを除いて)あらゆる可能性和了きるまで計算すると大変なことになる．例えば3向聴の場合，和了まで4牌ツモらなくてはならないが，model4ではmodel2と比べて4!(=24)倍の計算量が必要になる．聴牌形と和了形が重要なだけで，そこに到達するまではどんな順序でツモるか等関係ないのでmodel4は無駄な計算をしていることになる(他の要因も考えると厳密はそうでもないんだけど...)．

といってもまだ重いんだよなあ．特に向聴数が大きい序盤がメチャ重い．向聴数が大きいときは枝狩りを厳しくするとかしないとだめかも．

以前ここに載せた麻雀の最終順位の期待値ですが，実はバグがある．点数が接近すると順位の逆転現象が起きるのだ．なんで試しに得点期待値ベースではなく期待最終順位ベースで組もうと去年の式を入れたら見事におかしなことになった．

そうでなくても，正規分布なんて使わずもう実測データに基づいてもっと軽いもののにしようと考えた．期待最終順位は，局単位の点棒の移動の分布に依存するはずである．つまり1回の和了の特性を知る必要がある．

www.interq.or.jp/snake/totugeki/MJSIM0.htm
によると，得点分布は次のようになる．(赤が元データの1次補間，黒がスプライン補間)

<< Graphics`Spline`

pts = {{1000, 1037}, {2000, 1292}, {4000, 1242}, {8000, 736}, {12000, 

        244}, {16000, 40}, {32000, 6}};

Show[

    Graphics[{

        Hue[0], Line[pts], GrayLevel[0], Spline[pts, Cubic]

        }],

    PlotRange \[Rule] {{0, 32000}, {0, 1400}}, Frame \[Rule] True, 

    AxesLabel \[Rule] {"points", "samples"}, Axes \[Rule] True];

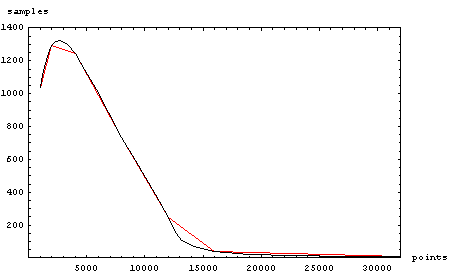
なかなか綺麗な分布である．これには流局時の点棒のやり取りがないが，できすぎ君によると流局率は15%程度なので(とつげき東北氏の成績)，まあ，こんな感じ？と都合よく流局も含めたグラフを作ってみる．

pts = {{0, 2040}, {1000, 1037 + 700}, {4000, 1242}, {8000, 740}, {12000, 

        244}, {16000, 40}, {32000, 6}};

Show[

    Graphics[{

        Hue[0], Line[pts], GrayLevel[0], Spline[pts, Cubic]

        }],

    PlotRange \[Rule] {{0, 32000}, {0, 2300}}, Frame \[Rule] True];

Plot[If[x < 14000, 2000 - 1900x/14000, 

    100 - 95(x - 14000)/(32000 - 14000)], {x, 0, 32000}, 

  PlotRange \[Rule] {{0, 32000}, {0, 2300}}]

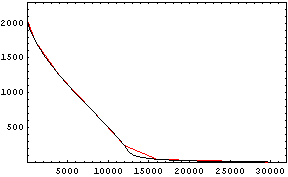
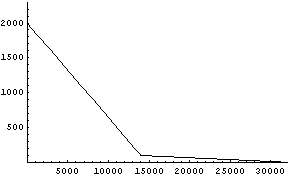
左がこんなもんだろうと作ってみたデータ，右がプログラム内で簡単に使えるように適当に作ったそれの1次近似*2である．
本当は失点分布も作りたいけど，データがないため得点分布と同じとしておこう(ツモられる事が多いので本当は横に縮んで縦方向に伸びる分布になるはずですが，まいいや)．それで，この分布をベースに期待最終順位のようなものを出してみよう．

ExpectOrder[m_] := Module[{a, p, r, s},

      updown[x_, p_] := 

        If[m[[p]] \[Equal] m[[x]], 0, If[m[[x]] < m[[p]], 1, -1]];

      RealOrder[p_] := 

        2.5 + (updown[p, 1] + updown[p, 2] + updown[p, 3] + updown[p, 4])/2;

      DisplayTogether[

        ListPlot[

          Table[{s,

              For[p = 1; q = a = 0, p \[LessEqual] 4, p++,

                d = Abs[s - m[[p]]];

                d *= 1.0Exp[-0/10]*If[p \[Equal] 2, 0.7, 1];

                         ↑残り局数や親番が残っているかで偏差を変える

                r = If[d < 14000, 2000 - 1900d/14000, 

                    100 - 95(d - 14000)/(32000 - 14000)];

                r = If[r > 0, r, 0];

                q += r;

                a += RealOrder[p]*r;

                ];

              a/q

              }, {s, 0, 50000, 1000}

            ],

          PlotJoined \[Rule] True],

        ListPlot[

          Table[{m[[p]], RealOrder[p]}, {p, 1, 4}],

          PlotStyle -> {Hue[0], PointSize[.02]}

          ],

        PlotRange \[Rule] {{0, 50000}, {1, 4}}, Frame \[Rule] True, 

        GridLines \[Rule] {m, Automatic},

        AxesLabel \[Rule] {"points", "Order"}, Axes \[Rule] True

        ];

      ];

ExpectOrder[{35000, 32000, 18000, 12000}]

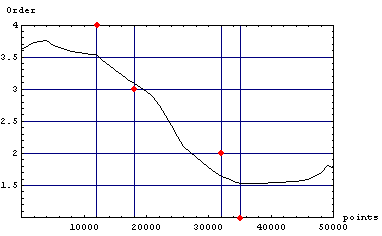
一応オーラス32000点持ちの2着が親という状況を想定．
各期待最終順位は順に 1.52986, 1.63943, 3.08817, 3.53771．

仮にここで3着が4着から跳満貫を和了っていると仮定すると，

ExpectOrder[{35000, 32000, 18000 +12000, 12000 - 12000}]

順位は 1.86527, 2.02736, 2.13788, 3.93874．
いい感じに三つ巴になっています．
順位の逆転が起きないしこれでよしとしよう．
(単調減少じゃないですが，青線上のデータしか使わないので関係ないはず．とはいえ気持ち悪いので直したいところ．もしかして有効桁数の問題か？)

といっても，オーラスは期待順位なんてものは計算にほぼ必要ないですが．

麻雀尽くし．．
こうやってwebにまとめておくと，1年経ってからでもすぐ参照して思考を再開できるので便利です．
一年前のmathematicaのnotebookなんてとっくに行方不明ですからね．
webに書いといて良かったー！

興味のない方ごめんなさい．