なにやら御大が批判されております．
まあ，こんな問題坂村先生にしてみれば瑣末な事ですけどね．全く気にしてないに違いない．あの勢いには我々一般庶民では太刀打ちできないのです．

ショッキングな事に既に東風荘の代打ちソフトがありました！
しかも牌譜付き．やられた．

予告編で，もの凄い勢いで聖書の暗号を解明してラビン暗殺やケネディ暗殺の謎に迫ります．
旧約の原書はヘブライ語です．ヘブライ語の文字は子音の周りに変な点等を付けてそれを母音とするのですが，普通本を書くときはその母音を省略します．日本語で漢字にいちいち読み仮名を振らなくても読めるように，彼らは母音が無くてもそれを読んでしまうわけです．てことでこじつけしまくりなんだな．あと折り返しとか使いまくってるし．
てか，同じ手法でうまくやればバイナリ列から預言を取り出す事ができるわけで，Windows95のkernel32.dllはイラク戦争を予知していた！ゲイツは神！とかなんでもできそうな予感．

カテゴリ別にログを取るようにしてみた．車輪の再発明しまくり．けどMTとかに移行する手間を考えたらcgi弄ったほうが早いししょうがない．

つまり，3sが4枚見えていたら全体的に1s2sは出易いだろうな，ということを計算したいのです．
これはもう前のversionでもやってたんだけど，今見たらかなりいい加減だったので修正してmathematicaで検証してみることにした．
といっても1-9の9種類の数牌に対してのみの検証．理論を確かめるならこれだけでも十分だと思うので．

In[]:= rest = {3, 3, 3, 3, 3, 3, 3, 3, 3};　←1-9の残り枚数　この場合は各1枚ずつ見えている

Clear[a, b, c, i, j, k, e];

a = b = c = Table[0, {i, 1, 9}, {j, 1, 5}];

e = Table[If[rest[[i]] \[Equal] j - 1, 1, 0], {i, 1, 9}, {j, 1, 5}] // N;

janto = 1;　←作る雀頭の数

mentsu = 6;　←作る面子の数



(*雀頭を取り除く*)

For[k = 0, k < janto, k++,

    t = 0;

    For[i = 1, i \[LessEqual] 9, i++,

      a[[i, 3]] = e[[i, 3]];

      a[[i, 4]] = e[[i, 4]]*3;

      a[[i, 5]] = e[[i, 5]]*6;

      ];

    t = Tr[Flatten[a]];

    For[i = 1, i \[LessEqual] 9, i++,

      e[[i, 1]] += a[[i, 3]]/t;

      e[[i, 2]] += a[[i, 4]]/t;

      e[[i, 3]] -= a[[i, 3]]/t + a[[i, 5]]/t;

      e[[i, 4]] -= a[[i, 4]]/t;

      e[[i, 5]] -= a[[i, 5]]/t;

      ];

    ];



(*補助関数*)

n[x_] := x[[2]]*1 + x[[3]]*2 + x[[4]]*3 + x[[5]]*4;

dec[e_, d_] := Module[{t, h},

      t = n[e]; h = e; If[d > 0,

        h[[1]] += d*1*e[[2]]/t;

        h[[2]] += d*2*e[[3]]/t - d*1*e[[2]]/t;

        h[[3]] += d*3*e[[4]]/t - d*2*e[[3]]/t;

        h[[4]] += d*4*e[[5]]/t - d*3*e[[4]]/t;

        h[[5]] +=              - d*4*e[[5]]/t;

        ];

      h];

dec3[e_, d_] := Module[{i, t, h},

      t = e[[4]]*3 + e[[5]]*4; h = e; If[d > 0,

        h[[1]] += d*3*e[[4]]/t;

        h[[2]] += d*4*e[[5]]/t;

        h[[4]] += -d*3*e[[4]]/t;

        h[[5]] += -d*4*e[[5]]/t;

        ];

      h];



(*面子を取り除く*)

a = b = Table[0, {i, 1, 9}, {j, 1, 5}];

For[k = 0, k < mentsu, k++,

    t = 0;

    For[i = 1, i \[LessEqual] 7, i++,

      a[[i, 1]] = n[e[[i]]]*n[e[[i + 1]]]*n[e[[i + 2]]];

      If[a[[i, 1]] > 0, t += a[[i, 1]]];

      ];

    For[i = 1, i \[LessEqual] 9, i++,

      b[[i, 4]] = 6*(e[[i, 4]]^3) + 24*(e[[i, 5]]^3);

      If[b[[i, 4]] > 0, t += b[[i, 4]]];

      ];

    If[t \[Equal] 0, Print[k + 1]; Break[]];

    For[i = 1, i \[LessEqual] 7, i++,

      e[[i]] = dec[e[[i]], a[[i, 1]]/t];

      e[[i + 1]] = dec[e[[i + 1]], a[[i, 1]]/t];

      e[[i + 2]] = dec[e[[i + 2]], a[[i, 1]]/t];

      ];

    For[i = 1, i \[LessEqual] 9, i++,

      e[[i]] = dec3[e[[i]], (b[[i, 4]])/t];

      ];

    ];



ListPlot[e2, PlotJoined \[Rule] True, PlotRange \[Rule] {{1, 9}, {0, 3}}]

Out[]=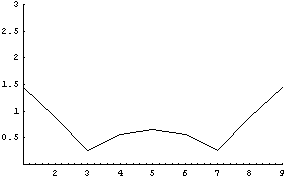

なげー．
アルゴリズムは各牌の残っている枚数を基に，どれが面子として使われてそうか確率を出して，その分枚数を減らしていくという感じ．
9種類の牌に対して0,1,2,3,4枚残っている可能性を別々に管理してるんでちょっと冗長．けど単に残っている枚数の期待値だけで管理していくと特定の状況の時正しく計算できないので仕方ない．

で，この例だと1=9>2=8>>>5>4=6>3=7の順で不要度が高い，つまりこぼれる可能性が高いと出た．ひいいさんの統計分析と違う結果ですが，これは1回1回自摸るのではなく，ざくっと3*9枚の牌を与えて適当に面子を作るシミュレートに近いので仕方ないかも．実際だと序盤に端牌が切れていくので，それを考慮すると似た様な結果になるのではないかと．
456より37が重要というのは奇妙な感じがするけど，1289という端牌を使って順子を作ろうと思うと必ず37が必要になるので，こうなるのが正しい気がする．実際37は要の牌とか言われるし(?)，麻雀放浪記かショーイチでも故意に対子場にするために37を固めて置くとかあった気がするし，やっぱ37が重要なんでしょう．46を握り潰すより37を握り潰した方が圧倒的に順子は作りにくくなるしね(前者では123,789の2通りの順子が作れるけど，後者は456しか作れない)．
(どうでもいいけど，「二五八は鳴くな，三六四七を鳴け」という格言があるらしい．二五八は終盤出易い筋で三六四七は出にくい筋なんだそうな．出典は自己中心派なんでアテになりませんが)

ついでに壁のある場合を試してみよう．

In[]:= rest = {2, 3, 0, 4, 4, 4, 4, 3, 2}; ←3が全て切れた状態

Out[]=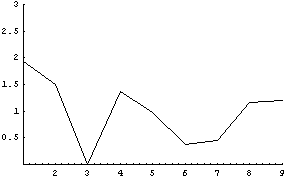

12がかなりの確率でこぼれる事が分かる．また，4は4枚生きているけど，2.5枚しか使い切れなくて1.5枚程こぼれると出る．よさげじゃないかい？

ただまだバグがあったりする．作る面子の数をぎりぎりまで多くしたりすると枚数の期待値が微妙にマイナスになることがあるのだ．てことでどっか間違ってるのは確かなのだけど，どこがダメなのか全然わかりません．