Appendix.A 多面体からなる剛体の質量と重心と慣性テンソル
シミュレータで扱う物体は質量や慣性テンソルが明らかな直方体や球ばかりではない．ここでは多面体の集合で表される密度一定な物体の質量と重心と慣性テンソルを導く．
A.1.体積
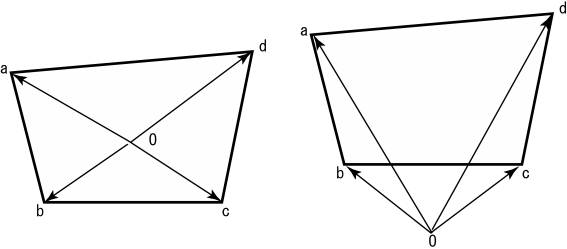
２次元の多角形の面積は３角形に分割して求めることが出来る．各頂点が反時計回りに配置してある場合ある１点と隣り合う頂点２つの３角形の面積の合計が面積である．例えば図のOabの面積は，
(A.1.1)
である．多角形の面積Sは
(A.1.2)
ある１点がもし多角形の外としても多角形外の部分は相殺されるためSは変わることはないし[1]，同様に凹形でも正しくSは求まる．
３次元空間の物体は３角錐の集合と考え同じ方法を適用する．図のa,b,cベクトルによる３角錐の体積は，
(A.1.3)
であり３角形と同様に時計回りの場合は値が負になる．なおこの式は４次元ベクトルの外積の1/6と等しい[2]．３角形の面の数だけ合計したものが最終的な体積となる．
(A.1.4)
A.2. 質量と質量重心
質量mは体積Vに単位体積辺りの質量
を乗ずればよい．
質量重心は個々の３角錐の質量と重心から求めることが出来る．重心Rは
なので，密度一定のベクトルa,b,cによる３角錐の重心は
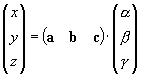
の変数変換を行い，
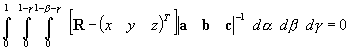
をRについて解いた
である．i個目の三角錐の質量と重心を
,
とするなら物体トータルの重心は
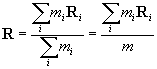
となる．
A.3. 慣性テンソル
慣性テンソルも重心と同じように個々の３角錐の慣性テンソルを計算し合計すればよいので，まず密度一定のベクトルa,b,cによる３角錐について考える．
(..)とA.2の変数変換を利用して
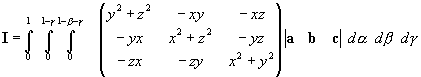
これを解いて
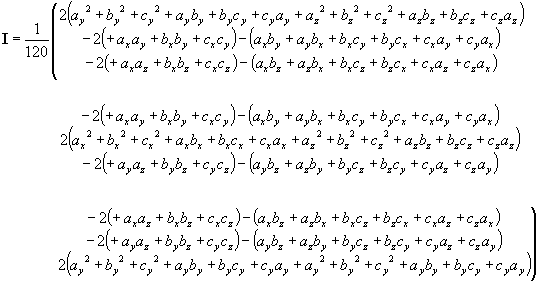
簡潔に表現するために
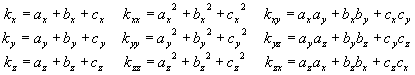
とおけば，
である．
は体積の6倍であるので質量と慣性テンソルを同時に計算していくと効率が若干良くなる．
i個目の三角錐の慣性テンソルを
とすれば，トータルの慣性テンソルは
となる．
B 主要形状の慣性テンソル一覧
/6