初歩のディジタルフィルタ
これはCGC代表のhTSがローパスフィルタを作りたいと言っていたので，それについて調子に乗っていい加減極まりない講義(?)もどきをした時のメモです．
学校の電気系の講義そのまんまやん！という突っ込みが入りそうですが，その通りです(笑)．
しかも「忘れまくっている＆z変換習ったばっかり＆音声信号処理の教科書を買って直に無くした(?)」ため間違っているところがあるかもしれません．
ここ間違ってるよ！勘違ってるよ！等の指摘よろしく．
アナログ回路からのアプローチ (RC回路)
フィルタといえばアナログ回路．例えば，安物のサウンドカードから高級アンプまで最終的な出力の手前には必ずローパスフィルタ(Low Path Filter ; LPF)付いています(多分)．どんなにディジタル処理全盛でも最後はアナログが重要になります．むしろディジタルの分解能が上がれば上がるほど重要になります，いや，なるかもしれません(弱気)．そんなわけで，アナログフィルタもバカに出来ないぞ！と思いつつその仕組みをある程度見ながら，コードに落としてみたいと思います．
先ずは手始めにLPFから．LPFというと難しそうな印象を受けるけど，実はただのRC直列回路だったりします(実際はオペアンプなんかも併用するけど，基本的にはRC，だよね．実は詳しく知りません．ごめん)．Rは抵抗，Cはコンデンサ(キャパシタとも言う)です，念のため．
このようにRC間に入力電圧を与えれば，C間の電圧はそれにローパスが掛かかったものになります．何でやねん！と思うかもしれないけど，キャパシタは電流を貯めて，その分端子間電圧が上がる性質があるためです．ってそれじゃ分からないか，まあ，きっとそのうち分かります(ぉ
で，そういった素子の性質を列挙すると，
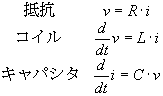
各式の定数はRが抵抗[Ω](オーム)，Lがインダクタンス[H](ヘンリー)，Cが静電容量[F](ファラデー)という単位．vは電圧[V]，iは電流[A]です．
では，図1の回路を定式化して
の形に整えてやればプログラムに落とせます．
に
を代入して，
つまり，
ここからがちょっと特殊だけど，
と変形してやると，
(キャパシタ間電圧)に関する微分方程式になります．これを離散化して式をまとめてやると，
の変化量に関する式が出てきます(差分方程式)．その式の中で
を使うのは反則のような気もするけど，
が極微小であればそれほど問題にならないので気にしない(ディジタル化する上でこれはどうしようもないのかも)．
これをCのコードに落とすと，x[n]を入力，y[n]を出力として
for(n=0;n<N;n++) {
out+=(x[n]-out)/R/C*dt;
y[n]=out;
}
これでLPF出来上がり．
実はバカらしくなるほどLPFは簡単なのです．dtはサンプリング周波数の逆数です．44100Hzのデータならdt=1/44100．
周波数特性は？
アナログ回路をディジタルフィルタに変換することはできたけど，その特性が分からないのはちょっと悲しい．実は周波数特性，及び位相特性はラプラス変換というのを使うと求まります．ラプラス変換を知らない人は，(このフィルタの説明に限っては)フーリエ変換と思っておけば問題ないです．
以下が各変換式
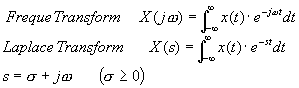
簡単に言えば，フーリエ変換では
が発散するような波形を変換することが出来ないけど，ラプラス変換ではσという波形を収束させるための変数(いや定数なのか?)を導入してどんな関数でも変換できるようにした，ということ．
え？フーリエ変換も知らない？そういう場合，式の数学的な意味は無視して，時間の関数を周波数の関数に変換する便利な公式くらいに考えておいて下さ．
で，
を，ラプラス変換してみると，
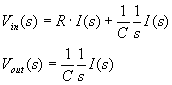
入出力の比を
，インパルス応答と定義します．
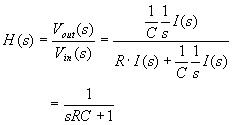
この比をここで，
より，
絶対値を取るとゲイン特性が分かります．
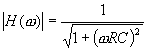
これらをmathematicaでグラフ化してみましょう(R=100[Ω],C=1[μF])．
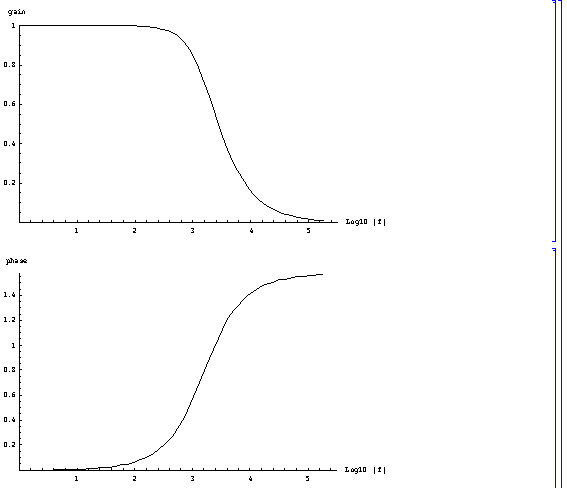
上がゲイン特性で，下が位相特性です．
x座標が10基底の対数になっているので分かりにくいかもしれませんが(人間は周波数が2倍で1オクターブ上がるといった具合に対数的に周波数を感じるため片対数グラフにしないとグラフの意味が掴み難い，しかしうまくx軸に数値を振る方法を知らなかったのでこれで勘弁して)，1000Hz付近からだんだんカットされるのが朧ながら分かると思います．
ここでゲイン特性を，
と
の二つに場合分けすると線形に近似できます．つまり
のときまでは減衰せず，それ以降のみ直線的に減衰するグラフに近時できます．この切り替わりの
を遮断周波数(正確にはこの式は角周波数なので
を掛けないと周波数じゃないけど)とか，カットオフ周波数などと呼びます．ちなみにそのときのゲインは
(=0.707…)．
今の例のカットオフ周波数は約628Hzとなります．確かにグラフで見る限りそんなもんですね．
あと，位相特性は….あまり重要じゃない気がするので特に気にしない方向で(ぉ さらに面倒なのでこの後グラフはゲイン特性しかプロットしません．悪しからず．
RLC直列回路
RC回路は簡単すぎて面白みが無いので，次はコイルを加えたRLC回路に挑戦してみましょう．
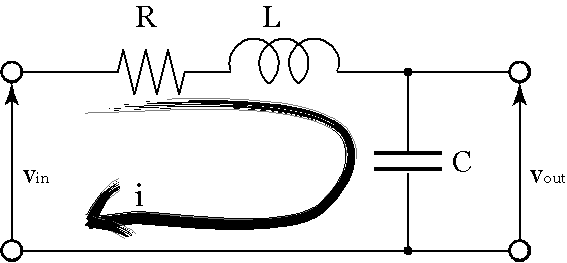
先と同じようにCの電圧を出力として式を立てます．
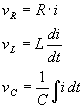
より，
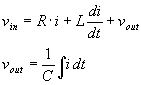
ここで先と同じように差分方程式へ持ち込むため微分形式にします．キャパシタの端子間電圧とコイルを流れる電流が微分形式になるように式を組み立てて，それを使って出力電圧を組み立てます．だからキャパシタとコイルの数だけ保持する変数があることになります．この場合だとコイルを流れる電流iとキャパシタ間電圧である
です．
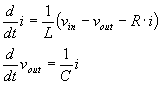
コードに落とすとこんな感じ．
for(n=0;n<N;n++) {
i+=(x[n]-out-R*i)/L*dt;
out+=i/C*dt;
y[n]=out;
}
保持する変数が１つ増えたけど相変わらず簡単．こんなんでいいのか？
さて周波数特性をみてみよう．
ラプラス変換して，
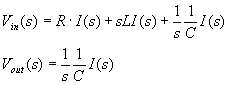
これより
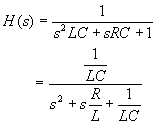
ここで，
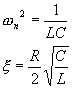
と置くと，(こうすると特性の解析が楽になる)
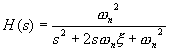
という式が求まるので，これでゲインを見てみよう．
(横軸はLog10[freq])
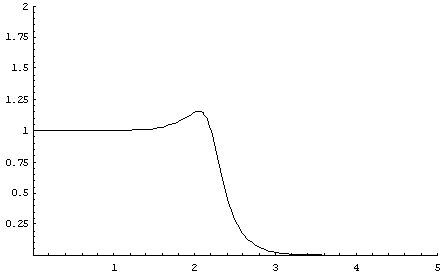
これより，
がRC回路でいうカットオフ周波数で，ξが小さいほどその周波数付近で共振することが分かります．レゾナンスですな．ゲインが1を超える場合があるので，コードに落とす際はオーバーフロー等に気をつけよう．
他にもLC並列の周波数選択等，単純だけど面白い回路を幾つかコードに落として試してみると良いかもしれません．頑張ればトランジスタなんかも再現できるはずなので(再現できても線形じゃないと思うのでラプラス変換して周波数特性を考えるのは無理だと思うけど)，往年のアナログシンセなんかを再現できるかもしれません．回路図があればの話だけど．
ディジタルフィルタの特性
と，RLC回路からフィルタを考えてみたのですが，別にそんなことしなくたって
for(n=0;n<N;n++) {
out=(x[n]+x[n+1])/2;
y[n]=out;
}
とかさあ，適当に組めば得体は知れないけどエフェクタが出来るじゃん．こういう場合はどうなるのさ？
という疑問が発生します．勿論こんなの回路じゃあり得ないし，ラプラス変換できるわけないし，周波数特性は不明？？と思うわけですが，やはり世の中凄い人がいて既にこういった離散的なフィルタの特性を求める変換を完成させています(単なる離散フーリエ変換，といってしまえばそれまでだけど)．それがｚ変換．アナログならラプラス変換，ディジタルならｚ変換を使うわけです．
で，そのz変換の定義式
普通はラプラス変換同様に
と，時間は0以降だけを考えます．これを片側ｚ変換といいます．といわれても，いちいち級数を考えろといわれても普通の人は凹んで諦めてしまいます．ので普通は変換表を使います．(ラプラス変換も普通は表を使うんだけど，あれは積分だからなんとかなる．一番良いのはMathematicaでLaplaceTransform,Ztransformという関数(package)を利用することか)
簡易変換表
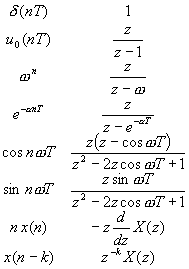
入力をx(n)，出力をy(n)とした場合，先ほどのコードは，
となります．z変換すると，
ラプラス変換同様にインパルス応答を求めてみましょう．
ここからラプラス変換だと，
と置いちゃうだけなんですが，z変換の場合は何故か
とします．なぜだ――ッ！？ と問い詰めたいところですが，これで周波数特性が分かるんですから，細かいことは気にせずに次行きましょう(ぉ
なので，
ゲイン特性は
Tにはサンプリング周波数の逆数を入れてやればよしなのでT=1/44100として，早速プロットしてみよう．
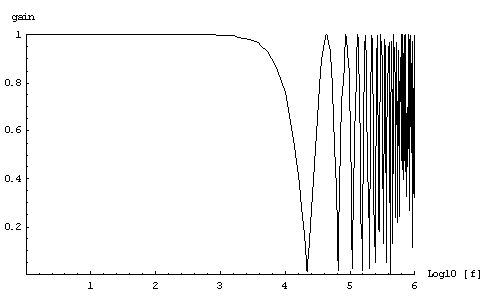
途中からcosが暴れていますが，よく考えたら44100Hzでサンプリングすれば22050Hzまでしかデータとして意味がありません．ということで，
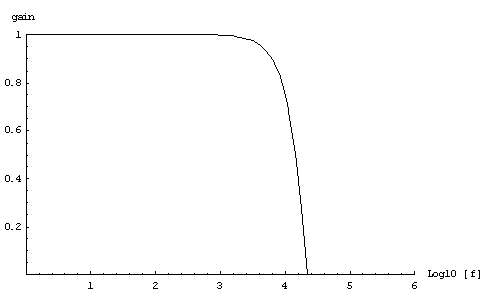
これがさっきのコードの周波数特性なわけです．見事なLPFです．RC回路よりストンと落ちてるあたりが素敵です．ただカットオフ周波数が高すぎて殆ど意味ないけど(笑)．
これを使うとアナログから強引にコードに落としたフィルタをz変換で検証できますね．暇な人はやってみよう(ぉ
と人任せも良くない気がするので，試しに最初のRC回路のコードを見てみましょう．
for(n=0;n<N;n++) {
out+=(x[n]-out)/R/C*dt;
y[n]=out;
}
これを数式にすると
になります．Z変換して特性を求めてみよう．
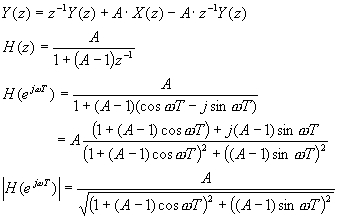
ゲイン特性をプロットすると，
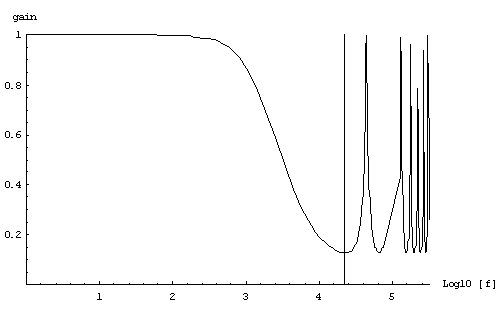
分かりにくいかもしれませんが，縦線が22050Hzです．それより右は無効です．見た感じ大体アナログの特性と同じですね．440Hzの時点ではアナログのゲインは0.963845，ディジタルは0.971708．その誤差0.82%．いい線いってるなあ，と思うけど，周波数が高くなると結構辛い．7040Hzだと17.45%の誤差．こうなってくると特性をちゃんとディジタルで再現しているかは微妙になってきます．もうちっとサンプリング周波数上げるか何かしないとまずいのかも．人間の可聴範囲のみを考えるなら44100Hzは十分すぎるけど，フィルタリングを考慮すると内部処理はもう少しオーダを増やした方が良いかもしれません．
FIRフィルタとIIRフィルタ
のようにy(n-k)という過去の出力を再利用する所謂フィードバックという奴を全く行わないフィルタを有限長インパルス応答--FIR(Finite – duration Impulse Response) フィルタと呼びます．
インパルスというのは「高さ無限大で，幅がなくて，面積が１」の波形のことです．全ての周波数を均等に含んでいるという特徴があります．なので，システムにこのインパルス(衝撃)を放り込んでやれば全ての周波数に対する応答が得られます(勿論システムが線形であればの話ですが，というかこのページの話は線形フィルタが大前提ですのでディストーションなんかは扱えません)．それがインパルス応答．
で，FIRはインパルスを放り込んでも出力が有限ということがいいたいだけです．
それに対して無限長インパルス応答---IIR(Infinite – duration
Impulse Response) フィルタというのも当然存在します．こいつはフィードバックを含むタイプです．なので少しでも入力があればえんえんと波形を出しつづけます．
これなんかそうですね．
と，用語のどうでもいい説明でした．